Công thức lượng giác hạ bậc cos2x , sin2x lớp 10 đầy đủ nhất

Các kiến thức về công thức hạ bậc cos2x , sin2x là một trong những kiến thức quan trọng được sử dụng phổ biến trong chương trình trung học phổ thông bắt đầu từ lớp 10. Để giúp các em học sinh có hệ thống kiến thức tốt hơn để áp dụng cho các bài thi nâng cao, chúng tôi sẽ chia sẻ trong bài viết này những Công thức hạ bậc cos2x , sin2x lớp 10, hãy cùng tham khảo và ghi nhớ nhé !  

Tại sao cần nắm được các kiến thức về hạ bậc cos2x , sin2x

Trong cuối chương trình lớp 10, các em học sinh sẽ được làm quen với chương lượng giác. Lượng giác là một nhánh của toán học, theo định nghĩa wikipedia thì là kiến thức dùng để tìm hiểu về về hình tam giác và sự liên hệ giữa cạnh của hình tam giác và góc độ của nó. Lượng giác chỉ ra hàm số lượng giác diễn tả các mối liên kết và có thể áp dụng được để học những hiện tượng có chu kỳ, như sóng âm.

Ngày nay khi nói đến lượng giác chúng ta sẽ thấy nó đặc biệt tập trung vào mối quan hệ giữa góc và chiều dài các cạnh tương ứng. Đồng thời các hàm lượng giác cũng tập trung vào những mối quan hệ trong đường tròn. Nhánh toán này được sinh ra từ thế kỷ thứ 3 trước công nguyên. Ban đầu nó là nhánh của toán hình học và được dùng chủ yếu để nghiên cứu thiên văn.[2] Lượng giác cũng là nền móng cho ngành nghệ thuật ứng dụng trong trắc địa.

Trong chương kiến thức về lượng giác lớp 10 này, các em sẽ học các kiến thức về cung và góc lượng giác. Đây là một phần kiến thức quan trọng và khá khó với nhiều em học sinh vì thế  để làm tốt các dạng bài tập về lượng giác yêu cầu các em phải nắm vững các công thức. Trong đó có các Công thức hạ bậc cos2x , sin2x lớp 10. Do đó, chúng tôi đã biên soạn các công thức lượng giác toán 10 đầy đủ nhất bao gồm các công thức lượng giác cơ bản và nâng cao mà chúng ta thường xuyên dùng để giải bài tập.

7 công thức hạ bậc cos2x , sin2x lớp 10

Công thức hạ bậc là gì ? Trong kiến thức lớp 10 công thức hạ bậc được hiểu là tìm cách để đưa các hàm số lượng giác có bậc cao về bậc thấp hơn. Với các hàm trong lượng giác thì chúng tôi tổng hợp có 7 cách hạ bậc tương đương với 7 công thức sau :

Ứng dụng công thức hạ bậc cos2x , sin2x lớp 10 làm một số bài tập

Bài tập 1

Cho 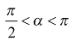 . Xác định tính âm dương của các giá trị lượng giác:

Hướng dẫn: Xác định điểm cuối của các cung ,… thuộc cung phần tư nào, từ đó xác định tính âm dương của các giá trị lượng giác tương ứng.

+ Cách xác định tính âm dương của các giá trị lượng giác

Giải

Áp dụng công thức hạ bậc ta có:

Bài tập 2

Áp dụng các công thức hạ bậc cos2x , sin2x lớp 10 giải các phương trình lượng giác sau:

Khi giải các phương trình lượng giác mà bậc của sin và cos là bậc chẵn ta thường hạ bậc từ đó đưa về phương trình cơ bản.

32. sin2x+sin22x+sin23x=32.
33. sin23x–cos24x=sin25x–cos26x.
34. sin2(x2–π4)tan2x–cos2x2=0.
35. cos23xcos2x–cos2x=0.

Từ sự xuất hiện bậc chẵn của hàm số sin và tổng hai cung 6x+2×2=4x mà ta nghĩ đến việc hạ bậc và sử dụng công thức biến tổng sang tích sau đó nhóm các hạng tử để đưa về phương trình tích.

PT⇔cos2x+cos4x+cos6x=0 ⇔cos4x(2cos2x+1)=0 ⇔[cos4x=0cos2x=–12

Vậy phương trình có nghiệm: x=π8+kπ4, x=±π3+kπ (k∈Z).

1. PT⇔1–cos6xx–1+cos8x2 =1–cos10x2–1+cos12x2

⇔(cos12x+cos10x) −(cos8x+cos6x)=0 ⇔2cos11xcosx–2cos7xcosx=0

⇔cosx(cos11x–cos7x)=0 ⇔cosxsin9xsin2x=0.

Vậy phương trình có nghiệm: x=kπ9, x=kπ2 (k∈Z).

1. Điều kiện: cosx≠0.

PT⇔12[1–cos(x–π2)]sin2xcos2x =12(1+cosx) ⇔(1–sinx)sin2x=(1+cosx)cos2x

⇔(1–sinx)(1+cosx)(sinx+cosx)=0.

Đáp số: Kết hợp với điều kiện ta được: x=π+k2π, x=–π4+kπ (k∈Z).

1. PT⇔1+cos6x2cos2x –1+cos2x2=0 ⇔cos6x.cos2x–1=0

⇔cos8x+cos4x–2=0 ⇔2cos24x+cos4x–3=0 ⇔cos4x=1⇔x=kπ2 (k∈Z).

Tại sao chúng ta cần học tốt môn lượng giác?

Một trong những kiến thức quan trọng của Lượng giác, mà chúng ta học được ở cuối lớp 10 và lớp 11 là các công thức đưa hàm sốc bậc cao về bậc thấp, không chỉ để giải bài tập mà còn ứng dung vào rất nhiều lĩnh vực của cuộc sống. Với nhiều học sinh thì thực sự đây là môn cực hình bởi nó có rất nhiều công thức và đa số các công thứ này đều rất khó nhớ. Và có thể bạn sẽ tự đặt câu hỏi tại sao chúng ta phải học môn này, nó có ứng dụng gì trong cuộc sống?

Tuy nhiên khác với suy nghĩ của nhiều người thì lượng giác quả thật có rất nhiều ứng dụng trong cuộc sống. Nhờ nó mà con người chúng ta đã làm được các điều kì diệu. Đầu tiên là thời Ai Cập cổ đại, họ đã phát triển lượng giác sơ khai để có thể xây dựng được Kim Tự Tháp, tạo ra đồng hồ mặt trời để xem thời gian. Về sau lượng giác còn được dùng để tính toán khoảng cách đến các ngôi sao gần. Trong thiên văn học.. Còn bây giờ thì lượng giác được ứng dụng vào rất nhiều ngành nghế như địa lý, lý thuyết âm nhạc, kinh tế học, điện tử học, lý thuyết xác suất thống kê, sinh học, y học, vật lý học, đồ hoạ máy tính, …  vân vân nhiều quá kể không hết.

Như vậy bài viết đã giới thiệu đến bạn tầm quan trọng cũng như một số Công thức hạ bậc cos2x , sin2x lớp 10. Hy vọng bài viết này giúp ích và tiếp thêm động lực cho bạn trong quá trình tiếp cận những kiến thức về bộ môn toán học thú vị này.